How to Read Repeated Measures Ancova Results Spss

General linear model which blends ANOVA and regression

"Ancova" redirects here. For the moth genus, meet Ancova (moth).

Analysis of covariance (ANCOVA) is a general linear model which blends ANOVA and regression. ANCOVA evaluates whether the means of a dependent variable (DV) are equal beyond levels of a categorical contained variable (Iv) often called a treatment, while statistically controlling for the effects of other continuous variables that are not of main involvement, known as covariates (CV) or nuisance variables. Mathematically, ANCOVA decomposes the variance in the DV into variance explained past the CV(south), variance explained by the chiselled IV, and residual variance. Intuitively, ANCOVA can exist idea of every bit 'adjusting' the DV by the group means of the CV(s).^[1]

The ANCOVA model assumes a linear relationship betwixt the response (DV) and covariate (CV):

${\displaystyle y_{ij}=\mu +\tau _{i}+\mathrm {B} (x_{ij}-{\overline {ten}})+\epsilon _{ij}.}$

In this equation, the DV, ${\displaystyle y_{ij}}$ is the jth observation under the ith categorical group; the CV, ${\displaystyle x_{ij}}$ is the jth observation of the covariate under the ith group. Variables in the model that are derived from the observed information are ${\displaystyle \mu }$ (the thousand hateful) and ${\displaystyle {\overline {10}}}$ (the global mean for covariate ${\displaystyle 10}$ ). The variables to exist fitted are ${\displaystyle \tau _{i}}$ (the upshot of the ithursday level of the Iv), ${\displaystyle B}$ (the gradient of the line) and ${\displaystyle \epsilon _{ij}}$ (the associated unobserved error term for the jth observation in the ith grouping).

Nether this specification, the categorical treatment effects sum to nix ${\displaystyle \left(\sum _{i}^{a}\tau _{i}=0\right).}$ The standard assumptions of the linear regression model are also assumed to hold, as discussed beneath.^[2]

Uses [edit]

Increment power [edit]

ANCOVA tin be used to increase statistical power (the probability a meaning divergence is found betwixt groups when one exists) by reducing the within-group error variance.^[3] In order to understand this, it is necessary to empathize the examination used to evaluate differences between groups, the F-test. The F-test is computed by dividing the explained variance between groups (e.1000., medical recovery differences) by the unexplained variance within the groups. Thus,

${\displaystyle F={\frac {MS_{betwixt}}{MS_{within}}}}$

If this value is larger than a disquisitional value, nosotros conclude that there is a significant deviation betwixt groups. Unexplained variance includes error variance (east.yard., individual differences), also equally the influence of other factors. Therefore, the influence of CVs is grouped in the denominator. When we command for the effect of CVs on the DV, we remove it from the denominator making F larger, thereby increasing your power to find a significant effect if one exists at all.

Adjusting preexisting differences [edit]

Another apply of ANCOVA is to adjust for preexisting differences in nonequivalent (intact) groups. This controversial application aims at correcting for initial group differences (prior to group assignment) that exists on DV amid several intact groups. In this situation, participants cannot be fabricated equal through random assignment, and then CVs are used to adjust scores and make participants more similar than without the CV. However, even with the use of covariates, there are no statistical techniques that can equate unequal groups. Furthermore, the CV may be so intimately related to the 4 that removing the variance on the DV associated with the CV would remove considerable variance on the DV, rendering the results meaningless.^[4]

Assumptions [edit]

There are several key assumptions that underlie the use of ANCOVA and affect interpretation of the results.^[2] The standard linear regression assumptions hold; further we assume that the slope of the covariate is equal across all handling groups (homogeneity of regression slopes).

Assumption i: linearity of regression [edit]

The regression relationship between the dependent variable and concomitant variables must exist linear.

Assumption two: homogeneity of fault variances [edit]

The error is a random variable with provisional naught mean and equal variances for different treatment classes and observations.

Assumption three: independence of error terms [edit]

The errors are uncorrelated. That is, the error covariance matrix is diagonal.

Assumption 4: normality of error terms [edit]

The residuals (fault terms) should be ordinarily distributed ${\displaystyle \epsilon _{ij}}$ ~ ${\displaystyle Due north(0,\sigma ^{2})}$ .

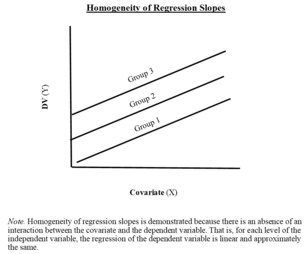
Assumption 5: homogeneity of regression slopes [edit]

The slopes of the different regression lines should be equivalent, i.e., regression lines should be parallel among groups.

The 5th issue, concerning the homogeneity of different treatment regression slopes is particularly important in evaluating the appropriateness of ANCOVA model. Too annotation that we only need the fault terms to exist commonly distributed. In fact both the independent variable and the concomitant variables volition not be normally distributed in most cases.

Conducting an ANCOVA [edit]

Examination multicollinearity [edit]

If a CV is highly related to another CV (at a correlation of 0.five or more), and so it will non adjust the DV over and higher up the other CV. I or the other should exist removed since they are statistically redundant.

Test the homogeneity of variance assumption [edit]

Tested by Levene'due south exam of equality of error variances. This is most important after adjustments have been fabricated, but if you lot take it before adjustment you are likely to accept information technology later on.

Test the homogeneity of regression slopes assumption [edit]

To run into if the CV significantly interacts with the IV, run an ANCOVA model including both the IV and the CVxIV interaction term. If the CVxIV interaction is meaning, ANCOVA should not be performed. Instead, Green & Salkind^[5] suggest assessing group differences on the DV at particular levels of the CV. Also consider using a moderated regression analysis, treating the CV and its interaction as another IV. Alternatively, one could utilize mediation analyses to determine if the CV accounts for the IV'south effect on the DV.

Run ANCOVA assay [edit]

If the CV×Four interaction is non meaning, rerun the ANCOVA without the CV×IV interaction term. In this analysis, you lot demand to use the adjusted means and adjusted MSerror. The adjusted ways (as well referred to as least squares means, LS means, estimated marginal means, or EMM) refer to the grouping means after decision-making for the influence of the CV on the DV.

Uncomplicated main effects plot showing a small Interaction between the two levels of the independent variable.

Follow-up analyses [edit]

If at that place was a significant main event, it means that there is a significant divergence between the levels of one IV, ignoring all other factors.^{[half dozen]} To find exactly which levels are significantly dissimilar from one some other, one can utilise the aforementioned follow-upwardly tests as for the ANOVA. If there are two or more IVs, at that place may exist a meaning interaction, which means that the effect of one IV on the DV changes depending on the level of another cistron. One can investigate the simple principal effects using the same methods as in a factorial ANOVA.

Ability considerations [edit]

While the inclusion of a covariate into an ANOVA generally increases statistical power past accounting for some of the variance in the dependent variable and thus increasing the ratio of variance explained by the contained variables, calculation a covariate into ANOVA too reduces the degrees of freedom. Accordingly, adding a covariate which accounts for very piddling variance in the dependent variable might actually reduce power.

See also [edit]

• MANCOVA (Multivariate analysis of covariance)

References [edit]

1. ^ Keppel, G. (1991). Pattern and analysis: A researcher's handbook (3rd ed.). Englewood Cliffs: Prentice-Hall, Inc.
2. ^ ^{a b} Montgomery, Douglas C. "Design and analysis of experiments" (8th Ed.). John Wiley & Sons, 2012.
3. ^ Tabachnick, B. Yard.; Fidell, L. S. (2007). Using Multivariate Statistics (5th ed.). Boston: Pearson Teaching.
4. ^ Miller, G. A.; Chapman, J. P. (2001). "Misunderstanding Analysis of Covariance". Journal of Abnormal Psychology. 110 (1): forty–48. doi:x.1037/0021-843X.110.1.40. PMID 11261398.
5. ^ Green, S. B., & Salkind, Due north. J. (2011). Using SPSS for Windows and Macintosh: Analyzing and Understanding Data (6th ed.). Upper Saddle River, NJ: Prentice Hall.
6. ^ Howell, D. C. (2009) Statistical methods for psychology (7th ed.). Belmont: Cengage Wadsworth.

External links [edit]

Wikiversity has learning resources virtually ANCOVA

• Examples of all ANOVA and ANCOVA models with up to iii treatment factors, including randomized cake, dissever plot, repeated measures, and Latin squares, and their analysis in R (University of Southampton)
• One-Fashion Assay of Covariance for Independent Samples
• What is analysis of covariance used for?
• Use of covariates in randomized controlled trials past M.J.P. Van Breukelen and 1000.R.A. Van Dijk (2007)

hoffmanwhatilly.blogspot.com

Source: https://en.wikipedia.org/wiki/Analysis_of_covariance

Share this post